Last Updated on 2025年2月18日 by 成田滋

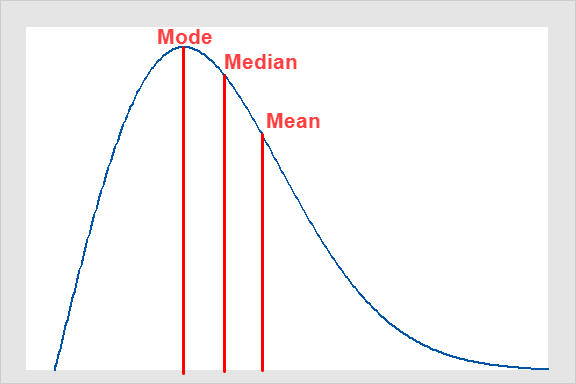
人間の多くの特性に関するデータなどは、いわゆる正規分布に近い値をとります。そのデータは平均値の近くに現れます。これを表すために曲線を描くと釣り鐘状の形になり、平均値(mean)、中央値(median)、最頻値(mode) は同じ点に表れます。このような分布で示される平均値は算術平均(arithmetic mean)といわれます。ですが人々の身長とか体重を表すのには同じように使えますが、人々の資産額の増加や減少の比率を表すのには適していません。この場合は、幾何平均(geometric mean) を使うほうが適しているのですが、ここでは触れません。

　ある地域のすべての家族の年間収入をリストアップするとします。そうすると、あまり高くない300万円から3000万円程度までの範囲に及ぶことがわかるとします。それをグラフで示すと、収入の散布は曲線の左側に大きく偏ります。釣り鐘状のように対称的ではなく、歪んで(skew)います。その形状は、はしごが急激に頂点まで上昇し、そこから徐々に下がっていきます。まるで子どもの滑り台のような形となります。平均値は中央値からかなり離れています。これにより収入の平均値と中央値を比較した場合、そのどちらを選ぶかによって収入の意味合いが異なってくるのです。

　Wikipediaによりますと、日本の国税庁の民間給与実態統計調査では、平成29年度の場合、給与所得の平均値は423万円で、最頻値は300万円～400万円の区分となり、少しずれています。従って、一般的な世帯の所得をとらえるには中央値や最頻値が有効であるとされています。

　もう一つの例ですが、不動産の売買では所在地が著しく違っているので、不動産の平均値は大きく異なります。例えば地方の田舎の住民のほとんどは、小規模農家か、そこで働く賃金労働者、年金生活の高齢退職者です。しかし、住民のうち 3 人は大金持ちであったとしますと、この 3人の総収入が住民の総収入の算術平均を大幅に押し上げます。同時に彼ら3人の収入は近所のほぼ全員の収入を押し上げます。これは比喩ではなく事実なのです。そして、ほぼ住民の全員が平均値以下となります。

　私たちが、例えばある企業が、そこでで働く人々の平均給与がこれこれであるという発表を読んだとします。給与の平均値が中央値であれば、そこから重要なことを学ぶことができます。従業員の半数はそれ以上の給与を稼ぎ、残りの半数はそれ以下の給与を稼いでいるということです。しかし、企業の全職員の構成などが明記されていない場合、つまり重役や事業主の給与と賃金労働者の給与の平均以上のことは何も明らかにしていないかもしれません。重役の平均総収入5,000万円の中には、2,000万円の給与の他に、事業から得た莫大な利益が含まれている可能性があります。重役や事業主の総収入が平均値を押し上げたり、非正規従業員の収入が平均値を押し下げたりするのです。このように平均値は、一体なにを示すのかを読み解くと合点がいかないことが生まれるものです。

　初任者の従業員から数100万円のボーナスをもらう社長まで、従業員の階層構造を持つ企業だとすれば、あらゆる種類のものがこのように隠蔽される可能性があるというわけです。従って、平均賃金の数字を見たら、まず「何の平均か？誰が含まれているか？」と自問することです。平均賃金とか賃金率については、いろいろな裏があります。例えば1 年間は半日勤務し、次の年はフルタイムで働けば、収入は 2 倍になります。しかし、それは賃金率についてはまったく何も語ってはいないのです。

　幾何平均は、時間に応じて変化する変化率／比率／倍率のデータの平均値を求める場合に、算術平均の代わりに用いられます。例えば、幾何平均は月ごとの人口増加率(変化率のデータ）の平均値を求めたり、年ごとの貯金利息率(比率のデータ）の平均値を求めたりするのに使われるのが一般的です。